You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 인장 시험 엑셀 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://toplist.pilgrimjournalist.com team, along with other related topics such as: 인장 시험 엑셀 0.2 offset 항복강도 엑셀, 인장시험 보고서, 인장시험 그래프 해석, 인장응력 그래프, 인장시험이란, 인장강도 탄성계수 관계, 인장 시험 시편
Table of Contents
[엑셀] Stress-strain 그래프 그리기 :: charming
- Article author: mint1397.tistory.com
- Reviews from users: 45539
Ratings
- Top rated: 3.7
- Lowest rated: 1
- Summary of article content: Articles about [엑셀] Stress-strain 그래프 그리기 :: charming [엑셀] Stress-strain 그래프 그리기 … 1. 인장시험으로 얻은 엑셀 그래프를 준비한다. 2. 삽입- 차트- 곡선이 있는 분산형을 클릭해 그래프를 만든다. 3. …
- Most searched keywords: Whether you are looking for [엑셀] Stress-strain 그래프 그리기 :: charming [엑셀] Stress-strain 그래프 그리기 … 1. 인장시험으로 얻은 엑셀 그래프를 준비한다. 2. 삽입- 차트- 곡선이 있는 분산형을 클릭해 그래프를 만든다. 3. 1. 인장시험으로 얻은 엑셀 그래프를 준비한다. 2. 삽입- 차트- 곡선이 있는 분산형을 클릭해 그래프를 만든다. 3. 그래프에서 마우스 우클릭-데이터 선택을 클릭한다. 4. 추가를 클릭해 계열 이름을 입력하고 X..
- Table of Contents:
![[엑셀] Stress-strain 그래프 그리기 :: charming](https://img1.daumcdn.net/thumb/R800x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FvTDwq%2FbtqEtNhJuys%2FY8cYs5IKLCx5k53jwoS9N0%2Fimg.png)
인장 시험 엑셀
- Article author: contents2.kocw.or.kr
- Reviews from users: 27841
Ratings
- Top rated: 4.4
- Lowest rated: 1
- Summary of article content: Articles about 인장 시험 엑셀 I. 인장 시험 (Tensile Test). 1) 시험 목적. ▫ 시험 → 하중-변형 (F-δ) → 응력- … 인장 시험 결과 데이터. 8. ② 엑셀 실행. ▫ 수식 상자(보기 > 수식 입력줄) … …
- Most searched keywords: Whether you are looking for 인장 시험 엑셀 I. 인장 시험 (Tensile Test). 1) 시험 목적. ▫ 시험 → 하중-변형 (F-δ) → 응력- … 인장 시험 결과 데이터. 8. ② 엑셀 실행. ▫ 수식 상자(보기 > 수식 입력줄) …
- Table of Contents:

인장시험 그래프 그리는 방법 좀 알려주세요..ㅜ – 인쇄골목묻고답하기 – 인쇄골목
- Article author: m.cafe.daum.net
- Reviews from users: 12069
Ratings
- Top rated: 4.5
- Lowest rated: 1
- Summary of article content: Articles about 인장시험 그래프 그리는 방법 좀 알려주세요..ㅜ – 인쇄골목묻고답하기 – 인쇄골목 엑셀로 그래프를 그리는 부분은 알려드리는 방법대로 주변 지인의 도움을 … YP는 항복점을 뜻합니다 (Yield Point) 보통 인장시험 하면 그래프가 … …
- Most searched keywords: Whether you are looking for 인장시험 그래프 그리는 방법 좀 알려주세요..ㅜ – 인쇄골목묻고답하기 – 인쇄골목 엑셀로 그래프를 그리는 부분은 알려드리는 방법대로 주변 지인의 도움을 … YP는 항복점을 뜻합니다 (Yield Point) 보통 인장시험 하면 그래프가 … 모든 이야기의 시작, Daum 카페
- Table of Contents:
인쇄골목묻고답하기
카페 검색

응력-변형률 선도 (Stress-Strain Diagram) – 영구노트
- Article author: satlab.tistory.com
- Reviews from users: 38372
Ratings
- Top rated: 3.5
- Lowest rated: 1
- Summary of article content: Articles about 응력-변형률 선도 (Stress-Strain Diagram) – 영구노트 1. 인장 시험 (Tension Test) 인장 시험은 재료의 역학적인 특성치를 결정하는 가장 기본적인 시험이다. 시험에 쓰이는 대상물은 시편(specimen), … …
- Most searched keywords: Whether you are looking for 응력-변형률 선도 (Stress-Strain Diagram) – 영구노트 1. 인장 시험 (Tension Test) 인장 시험은 재료의 역학적인 특성치를 결정하는 가장 기본적인 시험이다. 시험에 쓰이는 대상물은 시편(specimen), … 1. 인장 시험 (Tension Test) 인장 시험은 재료의 역학적인 특성치를 결정하는 가장 기본적인 시험이다. 시험에 쓰이는 대상물은 시편(specimen), 시험 쿠폰(test coupon)등으로 불린다. 인장 시험은 만능 시험..
- Table of Contents:
1 인장 시험 (Tension Test)
2 응력과 변형률 (Stress and Strain)
3 응력-변형률 선도 (Conventional Stress-Strain Diagram)
4 분석에 사용하는 응력-변형률 선도
부록 파손(Failure) 파괴(Fracture) 파단(Rupture)
티스토리툴바

재료시험: 단위변환 및 압축시험 그래프 그리기 : 네이버 블로그
- Article author: m.blog.naver.com
- Reviews from users: 29477
Ratings
- Top rated: 3.2
- Lowest rated: 1
- Summary of article content: Articles about 재료시험: 단위변환 및 압축시험 그래프 그리기 : 네이버 블로그 ㅎ ㅎ ㅠㅠ 평상시 보던 인장그래프(stress-strain curve)와 다르니깐요. … 원하는 그래프를 만들기 위해 엑셀 ABS함수를 이용해 position과 load … …
- Most searched keywords: Whether you are looking for 재료시험: 단위변환 및 압축시험 그래프 그리기 : 네이버 블로그 ㅎ ㅎ ㅠㅠ 평상시 보던 인장그래프(stress-strain curve)와 다르니깐요. … 원하는 그래프를 만들기 위해 엑셀 ABS함수를 이용해 position과 load …
- Table of Contents:
카테고리 이동
유진님의블로그
이 블로그
재료시험
카테고리 글
카테고리
이 블로그
재료시험
카테고리 글
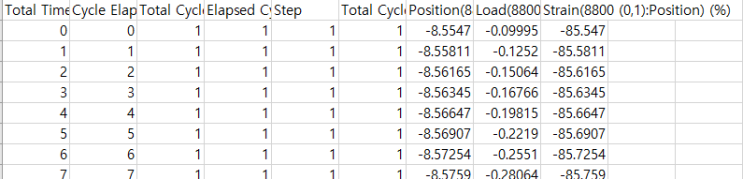
기계재료 인장시험 인장실험 결과보고서
- Article author: danasn.tistory.com
- Reviews from users: 13461
Ratings
- Top rated: 3.6
- Lowest rated: 1
- Summary of article content: Articles about 기계재료 인장시험 인장실험 결과보고서 기계재료 인장시험 인장실험 결과보고서 1. 실험결과 {Excel Data} 2. 결과분석 1) 인장강도와 파단강도 2) 항복강도와 탄성계수 3) 시험속도 4) … …
- Most searched keywords: Whether you are looking for 기계재료 인장시험 인장실험 결과보고서 기계재료 인장시험 인장실험 결과보고서 1. 실험결과 {Excel Data} 2. 결과분석 1) 인장강도와 파단강도 2) 항복강도와 탄성계수 3) 시험속도 4) … 기계재료 인장시험 인장실험 결과보고서 1. 실험결과 {Excel Data} 2. 결과분석 1) 인장강도와 파단강도 2) 항복강도와 탄성계수 3) 시험속도 4) 그래프 분석 * Necking현상 3. 파단면 분석 1) 연신율 2) 단면수..
- Table of Contents:
관련글
댓글0
최근글
인기글
티스토리툴바

See more articles in the same category here: Toplist.pilgrimjournalist.com/blog.
인장시험 그래프 그리는 방법 좀 알려주세요..ㅜ
Symbol YP-Load YP-Disp.
Dimension tf mm
1 9.2 1.78
Specimen 1
OriginalGL 50 mm Extenso.GL 50 mm
Ex.Diameter 12.5 mm
Area 122.7185 mm2
Number Load Stroke Elong Width
X 200msec tf mm mm mm
1 0 0 0 0
2 0 0 0 0
3 0 0 0 0
4 0 0 0 0
5 .005 .004 0 0
6 .015 .01 0 0
7 .025 .018 0 0
8 .035 .028 0 0
9 .04 .038 0 0
10 .045 .048 0 0
11 .05 .058 .00125 0
12 .055 .068 .00125 0
13 .06 .078 .00125 0
14 .07 .088 .00125 0
15 .075 .098 .00125 0
결과가 이런식으로 쭉 나왔는데…
보고서에 엑셀로 그래프를 만들어 오래요..
근데 위에 저게 무슨 말인지도 모르겠고..
엑셀도 할 줄 모르고..ㅜ
그래프 어떻게 그리죠???
질문자가 설택한 답변
엑셀 사용법을 여기서 가르쳐드리기에는.. 상당히 무리가 있고.. 양도 방대할 것 같네요.
위 결과에 대한 의미와 인장곡선을 그리는 방법만 가르쳐드리고
엑셀로 그래프를 그리는 부분은 알려드리는 방법대로 주변 지인의 도움을 받으시는 편이 훨씬
나을것이라 생각합니다. 그럼 위 결과의 의미와 그래프 작성 방법을 알려드릴게요.
Symbol YP-Load YP-Disp.
YP는 항복점을 뜻합니다 (Yield Point) 보통 인장시험 하면 그래프가 컴퓨터화면에 나타납니다.
그 그래프에 나타낸 표시가 항복점의 하중과 변위라는 의미로 보입니다.
Dimension tf mm
차원 즉 하중과 변위의 단위를 나타냅니다. 하중은 tonf이고 변위는 mm입니다.
1 9.2 1.78
이건 장비나 소프트웨어의 버젼을 뜻하는듯합니다. 인장시험결과에는 전혀 상관없으니 신경쓰실것 없구요.
Specimen 1
OriginalGL 50 mm Extenso.GL 50 mm
Ex.Diameter 12.5 mm
Area 122.7185 mm2
Number Load Stroke Elong Width
X 200msec tf mm mm mm
1번 시험편
Original Guage Length : 50mm, 연신율계(연신율측정장치)의 게이지 길이(Guage Length) : 50mm >> 연신율 측정을 위해 Extensionmeter라는 측정장치를 시험편에 부착합니다. 50mm간격으로 시험편의 두 지점에 물립니다. 시험편이 인장되면 부착된 연신율계가 벌어지게 되고 연신율을 측정합니다.
직경 : 12.5mm >> 시험편이 봉재일 경우 단면적을 계산하기 위해서는 직경을 알아야 합니다.
단면적 : pi/4*D^2 을 통해 구한 값.
번호 하중 스트로크 연신율 두께 >> 이 항목은 데이터의 항목을 나타냅니다. 즉 맨처음은 데이터 번호, 그 다음은 하중 스트로크 이런식으로요. 스트로크는 인장시험기의 Actuator, 즉 위의 로드셀은 가만히 있고 아래에 있는 액츄에이터가 움직이는데 이 때 액츄에이터가 초기 정지시 위치로부터 얼마나 이동했느냐 입니다. 두께는 측정장치가 없어 측정하지 않은 것 같은데 봉재 시험편의 경우 두께는 사용하지 않는 값입니다. 봉재의 인장곡선작성시에는 하중과 연신율만 있으면 됩니다.
1 0 0 0 0
2 0 0 0 0
3 0 0 0 0
4 0 0 0 0
5 .005 .004 0 0
6 .015 .01 0 0
7 .025 .018 0 0
8 .035 .028 0 0
9 .04 .038 0 0
10 .045 .048 0 0
11 .05 .058 .00125 0 >> 11번 데이터의 경우 : 번호 11 하중 0.05 스트로크 0.058 연신율 0.00125 두께 0
12 .055 .068 .00125 0
13 .06 .078 .00125 0
14 .07 .088 .00125 0
15 .075 .098 .00125 0
아마 위와 같은 데이터가 있는 Text 파일을 받으셨을 겁니다.
그 파일을 엑셀에서 열어 ‘띄어쓰기’로 데이터를 분류하면 한줄씩 데이터가 들어갑니다. 질문에는 띄어쓰기로
되어있습니다만 혹시 쉼표나 세미콜론으로 구분되어 있다면 그걸로 분류하시면 됩니다.
어떤 인장곡선을 그려오라 했는지 정확히 모르겠으나 인장곡선이라 함은 보통 하중-변위 선도보다는
응력-변형율 선도를 의미하므로 응력-변형률 선도 작성에 대해 알려드리겠습니다.
참고로 하중 변위 선도는 위 데이터중 하중과 스트로크만으로 그래프를 그리시면 그걸로 끝입니다 .
응력- 변형률 선도를 그리시려면 하중과 연신율을 제외한 나머지 항목을 삭제하시고
하중을 응력으로 바꿔주시면 됩니다. 변형률은 연신율과 동일합니다.
하중을 응력으로 바꿔주시려면 하중을 면적으로 나눠주시면 됩니다.
지금 하중이 tonf단위로 되어있으므로 1000을 곱하고 중력 가속도 9.81m/s^2을 곱해주어 N으로 바꿔줍니다.
그 값을 위에 나타나 있는 단면적으로 나눠주면 됩니다. 그러면 응력의 단위는 Mpa이 됩니다.(N/mm^2=Mpa)
엑셀에서 “=하중입력된셀선택*1000*4/pi/122.7185*9.81” 입력하시면 됩니다.
그리고 끝까지 쭈욱 드래그하셔서 수식을 모두 적용해주시면 모든 하중에 대한 응력이 구해집니다.
변형률은 연신율 자체가 변형률이므로 하중으로부터 구한 응력을 y축 변형률을 x축으로 하여
꺽은선형 그래프를 그리시면 됩니다.
참고하시구요
열공하세요^^
3172 엄마 아빠 결혼 기념일 선물,이모 생신선물 한결같이3 0 08.05.08 선물을 뭐 살지 고민이예요.부모님께…그리고 저희 이모도 생신인데,뭘 선물을…2795 부모님 결혼기념일선물이요 !…생각에는 엄마아빠결혼기념일선물로 디자인…1573 700일
3584 청첩장 디자인을 직접하고 인쇄만 부탁할 경우 인쇄비는 어느정도 인가요? 가을하늘 1 08.05.13 대부분 싸이트가 알아서 청첩장 인쇄…청첩장 주 이미지 인데요 인쇄만 따로…인쇄만 따로 할려는 경우 어느정도 비용이…지 궁금해요 청첩장 인쇄 비용에 대해 알고싶습니다 또한 청
3566 달력만들기,,, 총판 1 08.05.13 좀 아름다운 계절 달력이나 달력 사진…한결같이3 0 08.05.02 달력 의 종류 달력은 용도에…충무로에 가셔서 달력 210 달력,카렌다…카렌다제작
3478 구인구직 웹사이트 제작할 업체 구합니다. 예비신부 1 08.05.13 특정업(모델구인구직)에 종사하는 구인구직 웹사이트를 제작할려고 합니다….2) 새로운 구인구직 틀에서 나오는 디자인 기존은 구인구직 웹사이트 틀을 무시할순…일반 구인구직< b>
3510 명함사이즈요… 경은이 0 08.05.13 한판만 디자인하여 명함파일을 명함…단점은 다른 업체들의 명함과 함 27 명함정보…..사용법 ■ 명함< 2668 명함...공손히 전달한 명함< 3279 아파트 현관에 부착할 광고용 사이트나 광고,판촉업체 알려주세요. 재수 0 08.05.09 아파트 현관이나 엘리베이터에 보면 하단에 XX치킨 XX학원등 광고하는...추가된 질문 2006.10.29 06:27 추가 그리고 광고거울을 제작하는 업체나...393 전단지광고효력 하늘새 0 08 628 문자쿠폰을 문화상품권 싸이트에서 산다는데... ajflf 0 11:52 문화상품권 싸이트에서 문자쿠폰 살 수...저희 부모님이 이런 핸드폰 문자...걸 싫어하시는데 저는 문자가 너무...문자쿠폰이란 걸 사면 문자를 충전 할 수 있다길래요! 어
응력-변형률 선도 (Stress-Strain Diagram)
1. 인장 시험 (Tension Test)
인장 시험은 재료의 역학적인 특성치를 결정하는 가장 기본적인 시험이다. 시험에 쓰이는 대상물은 시편(specimen), 시험 쿠폰(test coupon)등으로 불린다. 인장 시험은 만능 시험기(Universal Test Machine, UTM)로 시험하며 만능 시험기는 일반적으로 시편을 잡을 수 있는 그립부가 있고 1축 방향으로 이동할 수 있는 자유도를 가지고 있다. 따라서 기본적으로 인장 시험과 압축 시험이 가능하며 시험 치구(test jig)를 적절히 설계하면 굽힘, 비틀림 등도 시험할 수 있다.
인장 시험의 기준 시편은 환봉(round bar) 형태이다. 그러나 최근 추세는 개뼉다구(dog bone) 형태의 평판 시편을 더욱 많이 쓰는 것으로 보인다. 아래 그림 1과 같은 환봉 형태의 시편이 있다면 단면이 일정한 부분에 gauge length를 설정하고 여기에 extensometer를 설치하여 gauge length가 늘어난 양 $\delta$를 측정하게 된다. 이 결과와 인장 시험기의 로드 셀(load cell)에서 얻은 하중 $P$를 이용해 하중-변위 곡선($P-\delta$ curve)을 얻는다. 많은 사람들이 인장 시험기에서 제공하는 변위(displacement)를 그대로 이용하여 하중-변위 곡선을 구하기도 한다. 그러나 개뼉다구 형상의 시편을 이용할 때는 시편을 붙잡는 그립(grip)부의 미끄러짐이 변위에 반영되어 적절한 결과를 얻지 못할 수 있다. 일단 적절한 하중-변위 곡선을 얻게 되면 시편의 형상 정보를 이용해 응력-변형률 선도(stress-strain diagram)로 변환하여 기계적 특성치를 얻는다.
그림 1. 인장 시편
2. 응력과 변형률 (Stress and Strain)
2.1. 응력 (Stress)
응력에는 공칭 응력(nominal stress)과 진응력(true stress)이 있다. 공칭이라고 하면 공연히 부르는 것을 말한다. 경제학에서 명목 GDP가 있고 실질 GDP가 있는 것처럼 응력에도 그냥 편하게 생각해서 대충 부르는 응력(공칭 응력)이 있고 진짜 찐 응력이 있는 것이다. 하지만 변형이 아주~ 작게 되면 이 대충 응력과 찐 응력이 거의 비슷하기 때문에 편하니까 대충 부르는 공칭 응력을 쓴다. 이렇게 뭔가 대충 넘어갈 때 engineering을 붙이면 된다. 따라서 공칭 응력은 engineering stress라고도 한다. 공학의 기본은 대충 그럴싸 하면 눈을 감고 넘기는 것이다. 공학은 비용 대비 이익을 추구하는 것이기 때문이다. 세세하게 따지면 그때부터는 과학이 된다. 요즘은 기계과(mechanical engineering)에서 재료과(material science)를 넘나들기 때문에 구분이 의미 있겠냐마는..
공칭 응력은 변형 전의 단면적을 이용해 계산한 응력이다. 실제로는 길이가 늘어나면서 단면적이 조금 줄어들테니 엄밀하게는 실제 응력과 차이가 있겠지만 변형이 아주 작다면 단면적도 비슷할 것이기 때문에 문제가 되지 않는다.
\begin{align} \bar{\sigma} &\equiv \frac{P}{A_0}: \text{nominal stress} \\\\ A_0 &= \frac{\pi d_0^2}{4}:\ \text{initial area} \end{align}
진응력은 변형 후의 단면적을 이용해 계산한 응력이다. 변형이 크면 단면적의 변화도 클 것이기 때문에 진응력을 이용해야 한다. 재료가 탄성 영역을 벗어나면 단면적이 급격하게 변하게 되므로 이때는 진응력을 이용해야 한다.
\begin{align} \sigma &\equiv \frac{P}{A}: \text{true stress} \\\\ A &= \frac{\pi d^2}{4}:\ \text{deformed area} \end{align}
2.2. 변형률 (Strain)
변형률에도 공칭 변형률(nominal strain)과 진 변형률(true strain)이 있다. 공칭 변형률은 변형 전 길이를 기준으로 변형률을 계산한다.
\begin{align} &\epsilon = \frac{L-L_0}{L_0} = \frac{\delta}{L_0}: \ \text{nominal strain} \\\\ &\delta = L-L_0:\ \text{elongation} \\\\ &L_0:\ \text{initial length} \end{align}
진변형률(true strain)은 변형 후 길이를 기준으로 계산한다. 실제 변형률이라고 할 수 있다.
\begin{align} &\bar{\epsilon} = \frac{L-L_0}{L} = \frac{\delta}{L}: \ \text{true strain} \\\\ &\delta = L-L_0:\ \text{elongation} \\\\ &L:\ \text{deformed length} \end{align}
따라서 미소 진변형률은 아래와 같이 쓸 수 있다.
$$ d\bar{\epsilon} = \frac{dL}{L} $$
이 미소 진변형률을 길이가 변화한 전체 구간에 대해 적분해보자.
\begin{align} \bar{\epsilon} &= \int_{L_0}^{L}\frac{dL}{L} \\\\ &= \left[ \ln L \right]_{L_0}^{L} \\\\ &= \ln\frac{L}{L_0} \\\\ &= \ln\left(\frac{L_0 + \delta}{L_0}\right) \\\\ &= \ln\left(1+\frac{\delta}{L_0}\right) \\\\ &= \ln(1+\epsilon) \end{align}
위 적분 결과로 공칭 변형률과 진변형률은 아래와 같은 관계가 있다는 것을 알 수 있다.
$$ \bar{\epsilon} = \ln(1+\epsilon) $$
만약 변형이 아주 작다면 공칭 변형률과 진변형률은 거의 같게 된다. 따라서 아주 작은 변형을 다루는 고체역학에서는 진응력과 진변형률을 사용하지 않는다. 하지만 변형이 크거나 소성을 고려한 분석을 할 때는 진응력과 진변형률을 이용해야 한다.
3. 응력-변형률 선도 (Conventional Stress-Strain Diagram)
3.1. 공칭 응력-변형률 선도 (Nominal Stress-Strain Diagram)
우리는 지금까지 인장 시험을 통해 하중-변위 곡선을 얻었고 이미 알고 있는 시편의 단면 형상과 초기 길이 정보를 이용해 응력-변형률 선도를 얻을 수 있었다. 일반적인 재료의 공칭 응력-변형률 선도를 그림 2에 나타냈다. 그림 2에서 x로 표시되어 그래프가 종료되는 곳이 재료가 두 동강 나는 지점이다. 취성재(brittle material)에 비해 연성재(ductile material)가 잘 늘어나는 성질이 있음을 보여준다. 자세한 내용은 다른 글에서 다루기로 한다.
그림 2. 기계 재료의 응력-변형률 선도
시편을 잡아당길 때 변형이 점점 커지면서 응력도 커지다가 어느 순간 재료가 더 이상 버틸 수 없는 지점에 이르면 재료에 파손(failure)이 발생한다. 이때의 응력 값을 특별히 강도(strength)라고 하며 이 값은 재료의 특성치이다. 강도에도 여러 종류가 있으니 아래에서 대표적인 기계 재료인 연강(mild steel)을 통해 알아보자.
강도(strength): 재료의 고유 특성치
응력(stress): $F/A$
3.2. 연강의 응력-변형률 선도 (Stress-Strain Diagram of Mild Steel)
기계 재료로 많이 사용되는 연강(mild steel)의 응력-변형률 선도를 그림 3에 나타냈다. 연강은 탄소 함유량이 비교적 적은 강재로 잘 늘어나는 성질을 가졌다. 잘 늘어난다고 하니 이상하게 느껴지겠지만 비교적 그런 것이고 탄소 함유량이 큰 고탄소강은 분필처럼 똑 부러진다. 물론 실제 부서질 때 소리는 똑이 아니라 벼락 치는 소리가 난다.
그림 3. 연강의 응력-변형률 선도. 검정색 선은 공칭 응력-변형률 선도이고 붉은색은 진응력-변형률 선도.
그림 3에 표시한 각 지점의 의미에 대해 하나씩 알아보자.
1) Point “A”: 비례 한계점(proportional limit point)
A점은 비례 한계점이라고 하고 이전까지의 영역은 변형률이 커지면 응력이 비례적으로 증가하는 비례 구간이다. 변형률이 이 비례 한계점을 넘으면 더 이상 응력은 변형률에 비례하지 않게 된다. 고체역학에서는 아주 작은 변형을 다루므로 비례 한계점 이내의 변형을 다룬다고 생각할 수 있다. 이 구간에서 선형 탄성 고체역학의 기계적인 물성(mechanical properties)을 결정한다.
a. 영률(Young’s modulus)
영률은 응력-변형률이 비례($\sigma \propto \epsilon$)하는 구간에서의 기울기이다. 탄성계수(elastic modulus, modulus of elasticity)라고도 한다. 이 구간에서는 응력이 변형률이 비례하므로 응력과 변형률의 관계는 다음과 같이 쓸 수 있다. 후크의 법칙(Hooke’s law)은 스프링에서 $P \propto \Delta$를 말하는 것이기는 하지만 고체역학에서 말하는 후크의 법칙은 응력과 변형률의 관계이다.
$$ \sigma=E\epsilon $$
b. 포아송 비(Poisson’s ratio)
포아송 비는 길이 방향의 변형률과 횡방향 변형률의 비율이다. 시편의 길이가 늘어난다면 길이에 수직한 방향인 폭은 줄어들게 되는데 인장 시편의 두 방향 변형률을 측정하여 구할 수 있다. 비율이기 때문에 단위는 무차원이다.
$$
u = -\frac{\text{lateral strain}}{\text{axial strain}} = -\frac{\epsilon_l}{\epsilon_a} $$
시편이 환봉이라면 비례 구간에서 아래처럼 각 축방향 변형률을 계산할 수 있다.
\begin{align} \epsilon_a &= \frac{\delta}{L_0} \\\\ \epsilon_l &= \frac{d-d_0}{d_0} \end{align}
c. 비례 한계 강도(proportional limit strength)
비례 한계점 A에서의 응력을 비례 한계 강도 ($\sigma_{\text{PL}}$)로 정의한다. 별로 쓸 일은 없다.
2) Point “B”: 상항복점(upper yield point)
상항복점은 상항복 강도(upper yield strength) $\sigma_y^u$가 결정되는 지점이다. 항복(yield)이라고 하는 것은 재료가 탄성을 잃고 소성 변형을 시작하는 점이다. 사실 비례 한계점을 넘는 순간 소성이 시작되는 것이지만 연강의 경우 그 바로 뒤에 특징적으로 꺾임(kink)이 존재하여 특별히 상항복점이라고 부른다. 하지만 이 상항복점은 시험 조건에 따라 값이 들쑥날쑥한 불안정(unstable)한 지점이기 때문에 기계적 물성으로 사용하는 것은 적절하지 않다.
일부 재료과에서 쓰는 교과서에는 상항복점을 그냥 항복점으로 표시하는 경우가 있는데 구조 설계의 관점에서 보지 않고 재료 그 자체만을 보기 때문인 것을 보인다.
3) Point “C”: 하항복점(lower yield point)
하항복점 상항복점에 비해 안정적으로 나타난다. 즉 시험할 때마다 비슷한 값이 나타난다. 따라서 이 점을 항복이 일어나는 점으로 하기로 하기로 하고 여기에서 항복 강도(yield strength)를 결정한다. 따라서 누가 그냥 항복점(yield point)라고 하면 하항복점을 말하는 것이다. 하항복 강도를 항복강도로 결정하면 상항복 강도보다 더 작기 때문에 항복 강도를 조금 더 보수적으로 결정하는 셈이다.
4) Point “D”: 극한점(Ultimate point)
극한점은 재료가 버틸 수 있는 최대 하중이 작용하는 지점이다. 이 부분은 공칭 응력-변형률 선도에서만 나타나는 것으로 진응력으로 그려보면 극한점이 변곡점이 되는 것을 알 수 있다. 이것은 단면적이 급격하게 작아지는 병목(necking) 현상이 이 지점에서 시작되기 때문이다. 병목 현상은 극한점에 다다른 재료가 꾸역꾸역 버티던 것을 포기하고 급격하게 늘어나면서 단면적 또한 급격히 작아지는 것이다. 이 때문에 변형 후 단면적을 이용하는 진응력 곡선에서는 응력이 계속해서 더 커지게 된다.
그림 4. Dogbone 시편의 인장 시험 중 변형 과정
이 지점에서 극한 인장 강도(ultimate tensile strength, $\sigma_{u}$)를 결정한다. 이 지점은 파괴점(fracture point)으로 병목(necking)이 시작되고 균열(crack)이 시작되는 지점으로 설계에서 반드시 피해야 한다.
5) Point “E”: 파단점(Rupture point)
파단점은 재료가 끊어지는 지점으로 파단 강도(breaking strength, \sigma_B)를 결정한다. 연강과 같은 연성재는 Lüders’ lines(or bands)를 따라 끊어진다. Lüders’ lines은 stretcher stain marks 또는 slip bands라고도 한다. 이 것은 연성재를 잡아당길 때 항복점 이후 시편에 약 45도 경사진 선이 나타나는 것으로 최대 전단 응력에 의해 재료가 파손된다는 실험적 검증이다. Lüders’ line이 발달하는 중에는 응력-변형률 선도에서 응력이 증가하지 않고 평탄하게 진행하거나 지글지글하게 수평으로 이동하고 Lüders’ line이 시편 전체를 관통하고 나면 응력이 증가하면서 극한점으로 진행한다. 이후 파단면은 Lüders’ line과 나란하게 발생한다.
그림 5. 연성재의 파단
취성재의 경우는 최대 주응력 방향으로 절단된다. 따라서 인장 축 방향과 90도 방향으로 나란하게 절단면이 형성된다.
그림 6. 취성재의 파단. 그림 죄송.
4. 분석에 사용하는 응력-변형률 선도
분석에서는 단순화한 응력-변형률 선도를 사용한다. 아래 몇 가지 주로 사용하는 응력-변형률 선도를 설명한다.
4.1. 탄성 재료(Elastic Material)
완전 탄성재는 항복을 고려하지 않는다. 상용 유한요소해석에서 선형 해석을 한다면 영률과 포아송 비 정도만 물성으로 입력하게 될 텐데 아래 그림 1과 같이 무한히 하중을 받을 수 있는 탄성 재료로 가정하는 것이다. 당연히 구조물의 거동이 탄성 영역에 있거나 소성이 발생해서는 안 되는 경우에 사용하고 이 모델을 사용한 구조물의 응력 항복강도를 초과하면 설계 변경이 필요하다.
그림 7. 완전 탄성 재료
4.2. 탄성/완전 소성 재료(Elastic/Perfectly Plastic Material)
이 모델은 완전 탄소성 재료 모델이라고도 하며 변형률 경화를 고려하지 않는 모델이다. 연강과 같은 연성 재료는 그림 3과 같은 거동을 한다. 탄성 구간을 지나 하항복점 이후에 잠시 평탄한 구간이 있는데 이 부분이 항복 구간이다. 이 항복 구간까지만을 고려하는 모델이다.
그림 8. 탄성/완전 소성 재료
4.3. 탄소성 재료(Elastic/Plastic Material)
변형경화 재료라고도 한다. 선형적으로 변형률 경화가 일어나는 모델이다. 그림 2에 표현된 연성 재료의 거동이 알루미늄과 같은 비철금속의 거동으로 이런 재료의 소성을 고려한 분석에서 주로 많이 쓰인다. 상용 유한요소해석 툴에서는 $E_1,\ E_2$와 같이 두 개의 영률을 받는데 항복 전과 후의 영률을 의미한다.
항복 이후의 소성 구간이 비선형인 소성변형 모델도 쓰이며 마그네슘 합금이 이에 해당한다.
그림 9. 탄소성 재료
4.4. 강성/완전 소성 재료(Rigid/Plastic Material)
탄성 영역에서 무한 강성 ($E = \infty$)을 갖지만 항복은 발생하는 재료이다. 이것은 탄성 변형률 $\epsilon_e$을 무시하는 모델이다. 소성 변형이 탄성 변형에 비해 압도적으로 클 때 사용할 수 있다.
$$ \epsilon = \epsilon_e + \epsilon_p \approx \epsilon_p \\\\ \because \epsilon_e << \epsilon_p$$ 그림 10. 강성/완전 소성 재료 4.5. 강소성 재료(Rigid Plastic Material) 소성 가공 분야에서 많이 사용하는 모델로 탄성 변형보다 소성 변형이 압도적으로 클 때 사용하며 변형률 경화까지 고려하는 모델이다. 변형률 경화 부분은 선형으로 할 수도 있고 비선형으로 할 수도 있다. 그림 11. 강성/소성 재료. 4.6. 조각 선형 재료 (Piecewise Linear Material) 실제 응력-변형률 선도를 조각 선형(piecewise linear)으로 이용하는 방법이 있다. 실제 선도를 조각내어 작은 구간 안에서는 직선으로 그어 선형적으로 이용하는 것이다. 상용 유한요소해석에서 물성을 표로 입력하여 이용할 수 있다. 하지만 이때는 반드시 진응력-변형률 선도를 넣어야 한다. 실제 단면적의 변화를 고려해야 하기 때문이다. 부록. 파손(Failure), 파괴(Fracture), 파단(Rupture) 파손(failure), 파괴(fracture), 그리고 파단(rupture)은 엄밀하게는 서로 다른 것으로 혼동하지 않도록 다시 한번 정리해서 알아 두자. 파손(failure)은 설계에서 의도했던 기능을 잃는 것이다. 시스템을 탄성 구간에서 설계했다면 탄성과 소성의 경계인 항복점에 도달하면 파손이 일어난다고 할 수 있다. 파괴(fracture)는 균열이 시작(initiation)되거나 이미 있는 균열이 진전(propagation)하면서 파손(기능의 상실)에 이르는 것이다. 신중하게 생각해야 할 것은 균열이 시작된다고 해서 반드시 두 동강 나는 것은 아니라는 것이다. 균열이 존재하더라도 더 이상 진전되지 않도록 설계하는 것도 가능하다. 실무를 하다 보면 많은 설계자들이 극한 인장 강도에서 재료가 뽀개지는 것으로 설명하곤 하는데 이는 엄밀히 말해서 잘못된 것이다. 극한 인장 강도에서는 파괴가 시작되는 것이고 뽀개지는 것은 파단(rupture)라고 한다.
So you have finished reading the 인장 시험 엑셀 topic article, if you find this article useful, please share it. Thank you very much. See more: 0.2 offset 항복강도 엑셀, 인장시험 보고서, 인장시험 그래프 해석, 인장응력 그래프, 인장시험이란, 인장강도 탄성계수 관계, 인장 시험 시편

