Top 21 이등변 삼각형 공식 Top 89 Best Answers

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 이등변 삼각형 공식 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://toplist.pilgrimjournalist.com team, along with other related topics such as: 이등변 삼각형 공식 이등변삼각형 넓이 공식, 이등변삼각형 밑변 공식, 이등변삼각형 각도 구하기, 이등변삼각형의 성질, 이등변삼각형 길이, 이등변 삼각형 길이 구하기, 이등변삼각형 높이 공식, 이등변삼각형 비율

[백점맞는수학] 초등5학년_삼각형의넓이

Table of Contents

이등변삼각형의 성질, 이등변삼각형이 되는 조건 – 수학방

Article author: mathbang.net
Reviews from users: 5950 Ratings
Top rated: 3.4
Lowest rated: 1
Summary of article content: Articles about 이등변삼각형의 성질, 이등변삼각형이 되는 조건 – 수학방 Updating …
Most searched keywords: Whether you are looking for 이등변삼각형의 성질, 이등변삼각형이 되는 조건 – 수학방 Updating 이제부터 본격적으로 도형과 도형의 성질에 대해서 알아볼 거예요. 우리가 알고 있는 도형들의 정확한 수학적 정의를 알아보고, 그 정의를 이용해서 증명도 해보죠. 증명된 명제는 정리로서 기억해야해요. 증명에..
Table of Contents:

이등변삼각형의 성질 이등변삼각형이 되는 조건

댓글(37개) 펼치기닫기

Article author: ko.wikihow.com
Reviews from users: 2548 Ratings
Top rated: 4.8
Lowest rated: 1
Summary of article content: Articles about 이등변삼각형 넓이 구하는 방법 (이미지 포함) – wikiHow Updating …
Most searched keywords: Whether you are looking for 이등변삼각형 넓이 구하는 방법 (이미지 포함) – wikiHow Updating 이등변삼각형 넓이 구하는 방법. 이등변삼각형은 두 변의 길이가 같은 삼각형입니다. 길이가 같은 두 변은 항상 같은 각도로 밑변(세 번째 변)과 연결되며, 정확히 밑변의 중점 위에서 만납니다. 길이가 같은 연필 두 자루와 자로 이 특성을 확인할 수 있습니다: 어느 한쪽의 각도를 기울이면 두 연필의 끝이 만나게 할 수 없습니다. 이등변삼각형의 이런 특성은 몇 가지 정보만으로 넓이를 구할 수 있게 합니다.
Table of Contents:

단계

팁

이등변삼각형의 성질, 이등변삼각형이 되는 조건

이제부터 본격적으로 도형과 도형의 성질에 대해서 알아볼 거예요.

우리가 알고 있는 도형들의 정확한 수학적 정의를 알아보고, 그 정의를 이용해서 증명도 해보죠. 증명된 명제는 정리로서 기억해야해요.

증명에 많이 사용되는 정의 중 가장 대표적인 게 삼각형의 합동조건이에요. 이 글에서도 삼각형의 합동조건을 계속 사용할 거니까 한 번 읽어보세요.

도형의 합동, 삼각형의 합동조건

이등변삼각형의 정의, 이등변삼각형의 성질

이등변삼각형은 두 변의 길이가 같은 삼각형이에요. 이등변삼각형에서 길이가 같은 두 변으로 이루어진 각을 꼭지각이라고 해요. 그리고 꼭지각이 아닌 다른 두 각을 밑각이라고 하고, 꼭지각의 대변을 밑변이라고 해요.

이등변삼각형의 성질

– 두 밑각의 크기가 같다.

– 꼭지각의 이등분선은 밑변을 수직이등분한다.

이등변삼각형이 무엇인지, 꼭지각과 밑각, 밑변은 어떤 것인지 대한 설명은 정의에 해당해요. 그리고 이등변삼각형의 성질은 참으로 밝혀진 명제, 즉 정리에 해당하죠. 정의와 정리의 차이를 알 수 있겠죠? 수학의 정의, 정리, 증명

그럼 참으로 밝혀진 명제인 이등변삼각형의 성질을 증명해볼까요. 일단 증명할 때는 가정과 결론, 증명으로 나눠서 해요.

이등변삼각형에서 두 밑각의 크기는 같다.

이등변삼각형이니까 두 변의 길이가 같아요. 이걸 가정으로 쓰고, “두 밑각의 크기가 같다”를 결론으로 하면 되네요.

가정: △ABC에서 이다.

결론: ∠B = ∠C이다

△ABC에서 꼭지각 ∠A의 각의 이등분선을 긋고 밑변과 만나는 점을 점 D라고 해보죠. 그러면 △ABD와 △ACD로 나뉘어요.

(1) (가정)

(2) ∠BAD = ∠CAD (∠A의 이등분)

(3) 는 공통

(1), (2), (3)에서 △ABD와 △ACD는 두 변의 길이와 그 끼인각이 같은 합동인 삼각형이에요. △ABD ≡ △ACD

따라서 대응각인 ∠B와 ∠C는 크기가 같죠. (증명 끝.)

이등변삼각형에서 꼭지각의 이등분선은 밑변을 수직이등분한다.

이등변삼각형이니까 두 변의 길이가 같고요. 꼭지각의 이등분선이라고 했으니까 둘로 나눈 각은 크기가 같겠죠? 이걸 가정과 결론으로 써보죠.

가정: △ABC에서 , ∠BAD = ∠CAD이다.

결론: , 이다

(1) (이등변삼각형, 가정)

(2) ∠BAD = ∠CAD (∠A의 이등분, 가정)

(3) 는 공통

(1), (2), (3)에서 △ABD와 △ACD는 두 변의 길이와 그 끼인각이 같은 합동인 삼각형이에요. (4) △ABD ≡ △ACD

대응변인 선분 BD와 선분 CD의 길이는 같죠. (5) 이다

그리고, 대응각인 ∠BDA와 ∠CDA도 같아요. ∠BDA = ∠CDA

그런데 이 크기가 같은 두 각을 더하면 평각인 ∠BDC가 돼요. ∠BDA + ∠CDA = 180° 결국 (6) ∠BDA = ∠CDA = 90°인 거죠.

(4)에 의해 가 되고, (6)에 의해서 가 됩니다. (증명 끝.)

이등변삼각형이 되는 조건

이등변삼각형이 어떤 삼각형인지 어떤 성질이 있는지 알아봤어요.

이번에는 반대로 어떤 삼각형이 있는데, 이게 이등변삼각형인지 아닌지 알아보려고 해요. 어떻게 알 수 있을까요?

이등변삼각형의 성질을 거꾸로 하면 돼요. 이등변삼각형은 두 밑각의 크기가 같다고 했어요. 이걸 거꾸로 해서 세 내각 중 두 내각의 크기가 같은 삼각형이 이등변삼각형인 거죠.

이등변삼각형이 될 조건 – 두 내각의 크기가 같은 삼각형은 이등변삼각형

이것도 가정과 결론으로 나누어 증명해보죠.

가정: △ABC에서 ∠B = ∠C

결론:

△ABC에서 ∠A의 각의 이등분선을 긋고 밑변과 만나는 점을 점 D라고 해보죠. 그러면 △ABD와 △ACD로 나뉘어요.

(1) ∠BAD = ∠CAD (∠A의 이등분)

(2) 는 공통

모든 삼각형 내각의 합은 180°에요. △ABD의 내각의 합과 △ACD의 내각의 합은 같죠.

∠BAD + ∠B + ∠ADB = ∠CAD + ∠C + ∠ADC인데, (1) ∠BAD = ∠CAD와 가정 ∠B = ∠C에 의해서 (3) ∠ADB = ∠ADC가 돼요. 결국 두 삼각형에서 세 각의 크기가 서로 같아요.

(1), (2), (3)에 의해서 △ABD와 △ACD는 한 변의 길이와 그 양끝각이 같은 합동이지요. (4) △ABD ≡ △ACD.

따라서 대응변인 선분 AB와 선분 AC의 길이가 같아요. (증명 끝.)

다음 그림에서 x를 구하여라.

그림에 보면 선분 AB와 선분 AC의 길이가 같다고 표시되어 있네요. 즉 이등변삼각형이에요. 이등변삼각형에서 밑각의 크기는 서로 같아요.

삼각형 내각의 크기의 합은 180°인데, 한 각은 110° 다른 두 같은 x로 크기가 같아요.

x + x + 110 = 180

x = 35(°)

정리해볼까요 이등변삼각형: 두 변의 길이가 같은 삼각형 이등변삼각형에서 두 밑각의 크기는 같다.

이등변삼각형에서 꼭지각의 이등분선은 밑변을 수직이등분한다. 두 밑각의 크기가 같으면 → 이등변삼각형

그리드형(광고전용)

직각 이등변 삼각형

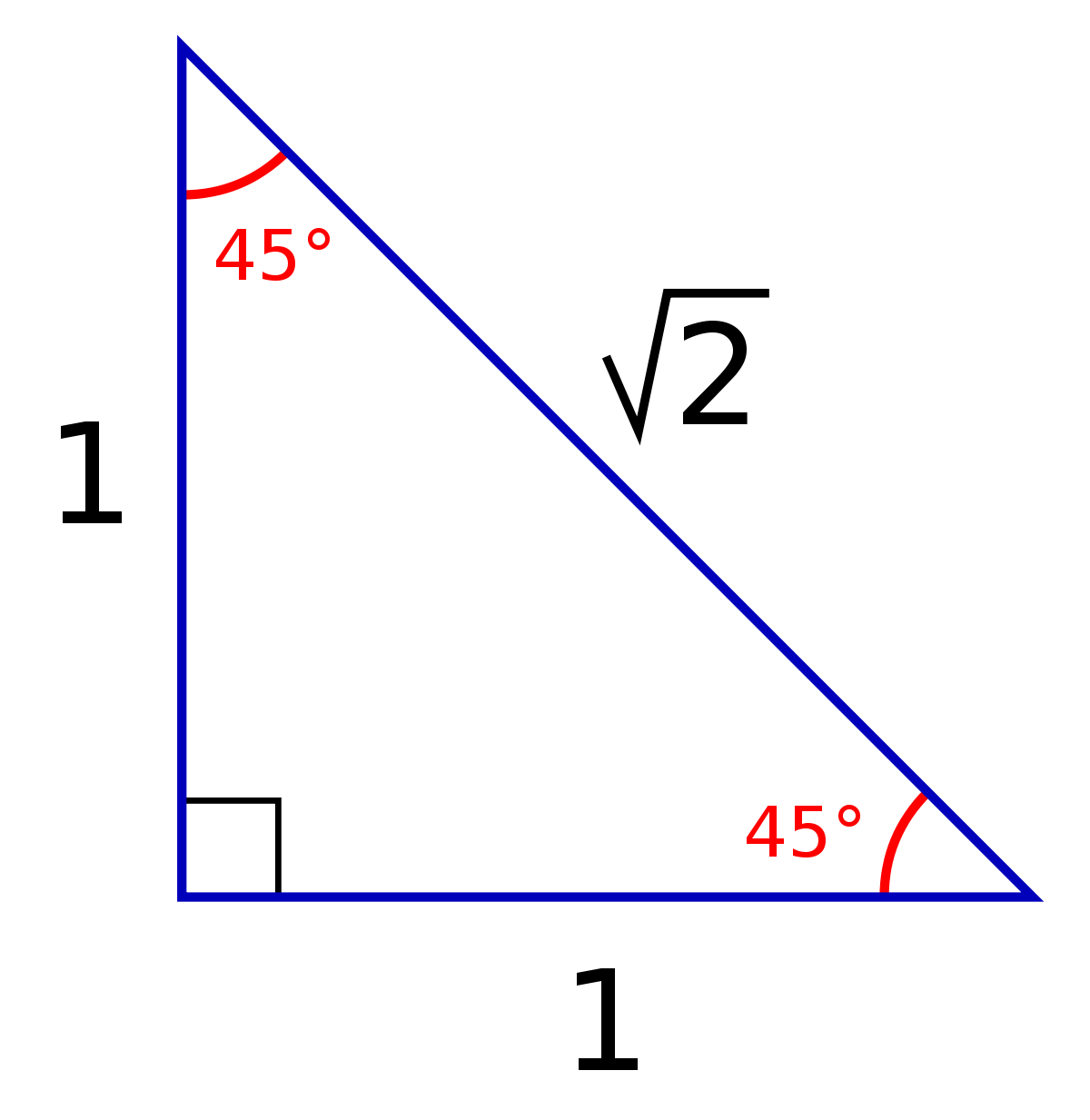
직각 이등변 삼각형의 각 변의 비를 보여준다.

기하학에서 직각 이등변 삼각형(直角二等邊三角形 , 英 : isosceles right angle)은 두변의 길이가 같으면서 길이가 서로 같은 두 변 사이의 각이 90도인 삼각형을 말한다. 직각삼각형이면서 이등변삼각형이라서 이런 이름이 붙여졌다. 직각 이등변 삼각형에서는 각 각의 비가 1 : 1 : 2 {\displaystyle 1:1:2} 이다. 삼각형에서 세 각의 합이 180도이므로, 두각의 크기는 45도이고 다른 각의 크기는 90도이다. 두 변의 길이의 비는 다음과 같다.

1 : 1 : 2 {\displaystyle 1:1:{\sqrt {2}}}

이것을 쉽게 증명하자면 변의 길이가 x {\displaystyle x} , y {\displaystyle y} , z {\displaystyle z} 인 삼각형이 있다고 해보자. 이 삼각형의 각 각의 크기가 45, 45, 90도라고 가정할 경우 삼각형 a b c {\displaystyle abc} 는 두각의 크기가 같으므로 이등변삼각형이 되고, 그래서 길이가 같은 변의 길이를 a {\displaystyle a} 이라고 가정한다면 피타고라스의 정리에 의하여

2 a 2 = 2 a {\displaystyle {\sqrt {2a^{2}}}={\sqrt {2}}a} 가 되기 때문이다.

정사각형을 대각선 따라 자르면 서로 합동인 두 개의 직각 이등변 삼각형이 나온다. 그리고 직각 이등변 삼각형을 대칭축에 따라서 잘라도 역시 서로 합동인 두 개의 직각 이등변 삼각형이 나온다.

성질 [ 편집 ]
직각 이등변 삼각형의 둘레는 다음과 같다.

빗변의 길이를 알경우 둘레는 2 a + a {\displaystyle {\sqrt {2}}a+a}

빗변이 아닌 다른 변을 알경우의 둘레는 다음과 같다. 2 a + 2 a {\displaystyle 2a+{\sqrt {2}}a}

직각 이등변 삼각형의 넓이는 다음과 같다.

빗변의 길이를 알 경우 넓이는 a 2 4 {\displaystyle {\frac {a^{2}}{4}}}

다른 변을 알 경우 넓이는 a 2 2 {\displaystyle {\frac {a^{2}}{2}}}

직각 이등변 삼각형과 놀이 [ 편집 ]

So you have finished reading the 이등변 삼각형 공식 topic article, if you find this article useful, please share it. Thank you very much. See more: 이등변삼각형 넓이 공식, 이등변삼각형 밑변 공식, 이등변삼각형 각도 구하기, 이등변삼각형의 성질, 이등변삼각형 길이, 이등변 삼각형 길이 구하기, 이등변삼각형 높이 공식, 이등변삼각형 비율

Top 21 이등변 삼각형 공식 Top 89 Best Answers

이등변삼각형의 성질, 이등변삼각형이 되는 조건 – 수학방

이등변삼각형 넓이 구하는 방법 (이미지 포함) – wikiHow

스크린골프 : 네이버 블로그

직각 이등변 삼각형 – 위키백과, 우리 모두의 백과사전

이등변삼각형의 성질, 이등변삼각형이 되는 조건

직각 이등변 삼각형

Leave a Comment Cancel reply