You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 구의 겉 넓이 적분 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://toplist.pilgrimjournalist.com team, along with other related topics such as: 구의 겉 넓이 적분 구의 겉넓이 구분구적법, 구의 겉넓이 공식, 구의 표면적 공식, 구의 겉넓이 중학교, 구의 부피 공식 증명, 구의 넓이, 반구 겉넓이, 원기둥의 겉넓이 공식
Table of Contents
구의 겉넓이 구하는 법 – 구의 겉넓이 공식 유도
- Article author: color-change.tistory.com
- Reviews from users: 47716
Ratings
- Top rated: 3.5
- Lowest rated: 1
- Summary of article content: Articles about 구의 겉넓이 구하는 법 – 구의 겉넓이 공식 유도 Updating …
- Most searched keywords: Whether you are looking for 구의 겉넓이 구하는 법 – 구의 겉넓이 공식 유도 Updating 구의 겉넓이 구하는 법 – 구의 겉넓이 공식 유도 이 포스팅은 구의 겉넓이의 공식 유도에 관한 글 입니다. 구의 겉넓이는 4πR²으로 그 결과만 알려줄 뿐 학교에서도, 학원에서도 증명해주지 않는 부분..
- Table of Contents:
고정 헤더 영역
메뉴 레이어
검색 레이어
상세 컨텐츠
태그
추가 정보
페이징
구의 겉넓이와 부피 – Wanho Choi
- Article author: wanochoi.com
- Reviews from users: 35538
Ratings
- Top rated: 4.9
- Lowest rated: 1
- Summary of article content: Articles about 구의 겉넓이와 부피 – Wanho Choi Updating …
- Most searched keywords: Whether you are looking for 구의 겉넓이와 부피 – Wanho Choi Updating
- Table of Contents:
Published by wano
Post navigation
Categories
Tags
Categories
Tags

지식저장고(Knowledge Storage) :: 구의 겉넓이와 부피
- Article author: mathphysics.tistory.com
- Reviews from users: 33033
Ratings
- Top rated: 4.9
- Lowest rated: 1
- Summary of article content: Articles about 지식저장고(Knowledge Storage) :: 구의 겉넓이와 부피 구의 겉넓이와 부피 중학교 때 반지름이 \(r\)인 구의 겉넓이는 \(4\pi … 미분하면 겉넓이가 되고, 겉넓이를 반지름에 대해 적분하면 부피가 된다. …
- Most searched keywords: Whether you are looking for 지식저장고(Knowledge Storage) :: 구의 겉넓이와 부피 구의 겉넓이와 부피 중학교 때 반지름이 \(r\)인 구의 겉넓이는 \(4\pi … 미분하면 겉넓이가 되고, 겉넓이를 반지름에 대해 적분하면 부피가 된다. 구의 겉넓이와 부피 중학교 때 반지름이 \(r\)인 구의 겉넓이는 \(4\pi r^{2}\)임이 알려져 있고, 부피는 구를 정사각형으로 분해한 다음 그 분해된 정사각형을 밑면으로 하고, 높이가 \(r\)인 사각뿔들의 합이..
- Table of Contents:
구의 겉넓이와 부피
구의 겉넓이와 부피
티스토리툴바

구의 부피 / 겉넓이 공식 정리 (+예시 풀이)
- Article author: alive-earth.com
- Reviews from users: 8159
Ratings
- Top rated: 4.4
- Lowest rated: 1
- Summary of article content: Articles about 구의 부피 / 겉넓이 공식 정리 (+예시 풀이) 저 공식은 “적분”을 이용해서 구한 공식인데요. 아직까지 미분 / 적분을 이야기 하는 것은 너무 심오한 이야기가 되기에, 간단하게 구의 부피와 겉넓이는 … …
- Most searched keywords: Whether you are looking for 구의 부피 / 겉넓이 공식 정리 (+예시 풀이) 저 공식은 “적분”을 이용해서 구한 공식인데요. 아직까지 미분 / 적분을 이야기 하는 것은 너무 심오한 이야기가 되기에, 간단하게 구의 부피와 겉넓이는 … 안녕하세요. 훈릴스입니다. 오늘은 구의 부피와 겉넓이를 구하는 공식에 대해 알아보는 시간을 가져보고자 합니다. 공식이 어려운 것은 아닌데 자꾸 잊어버리는 분들이 많을 것으로 생각됩니다. 저와 오늘 같이 정..
- Table of Contents:
Q 반지름이 2인 구가 있다 이 구의 부피와 겉넓이는 어떻게 되는가
태그
관련글
댓글0
공지사항
최근댓글
티스토리툴바
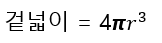
구의 부피와 구의 겉넓이 – 수학방
- Article author: mathbang.net
- Reviews from users: 4975
Ratings
- Top rated: 3.5
- Lowest rated: 1
- Summary of article content: Articles about 구의 부피와 구의 겉넓이 – 수학방 구의 부피와 구의 겉넓이. 구는 축구공, 배구공처럼 둥근 공 모양을 구하고 하지요? 구는 밑면, 옆면 구분이 없어요. 그래서 전개도로 펼쳐서 구하지 않아요. …
- Most searched keywords: Whether you are looking for 구의 부피와 구의 겉넓이 – 수학방 구의 부피와 구의 겉넓이. 구는 축구공, 배구공처럼 둥근 공 모양을 구하고 하지요? 구는 밑면, 옆면 구분이 없어요. 그래서 전개도로 펼쳐서 구하지 않아요. 이 글에서 공부할 내용은 구의 부피와 구의 겉넓이입니다. 구의 부피와 구의 겉넓이 구는 축구공, 배구공처럼 둥근 공 모양을 구하고 하지요? 구는 밑면, 옆면 구분이 없어요. 그래서 전개도로 펼쳐서 구하지 않아..
- Table of Contents:
구의 부피와 구의 겉넓이
댓글(35개) 펼치기닫기
구의 겉넓이 공식을 적분하면 부피 공식이 된다. — 우연일까? – 수학의 이론및 정리 – 재현고등학교 수학 좋은글과 희망
- Article author: m.cafe.daum.net
- Reviews from users: 2525
Ratings
- Top rated: 3.3
- Lowest rated: 1
- Summary of article content: Articles about 구의 겉넓이 공식을 적분하면 부피 공식이 된다. — 우연일까? – 수학의 이론및 정리 – 재현고등학교 수학 좋은글과 희망 구의 겉넓이 공식을 적분하면 부피 공식이 된다. — 우연일까? 구의 겉넓이 공식과 부피 공식. 반지름이 R인 구의 겉넓이와 구의 부피 공식은 다음과 같습니다. …
- Most searched keywords: Whether you are looking for 구의 겉넓이 공식을 적분하면 부피 공식이 된다. — 우연일까? – 수학의 이론및 정리 – 재현고등학교 수학 좋은글과 희망 구의 겉넓이 공식을 적분하면 부피 공식이 된다. — 우연일까? 구의 겉넓이 공식과 부피 공식. 반지름이 R인 구의 겉넓이와 구의 부피 공식은 다음과 같습니다. 모든 이야기의 시작, Daum 카페
- Table of Contents:
수학의 이론및 정리
카페 검색

See more articles in the same category here: https://toplist.pilgrimjournalist.com/blog.
구의 겉넓이 구하는 법
728×90
구의 겉넓이 구하는 법 – 구의 겉넓이 공식 유도
이 포스팅은
구의 겉넓이의 공식 유도에 관한 글 입니다.
구의 겉넓이는 4πR²으로 그 결과만 알려줄 뿐 학교에서도, 학원에서도 증명해주지 않는
부분이라 한번 쯤은 궁금하셨을 겁니다.
그 이유는 구의 겉넓이는 대학교 때 배우는 이중적분이라는 개념을 이용해 구할 수 있기 때문입니다.
이 글에서는 구의 겉넓이를 구하는 데 사용되는 이중적분의 개념을
다소 직관적이고 이해하기 쉬운 방법으로 설명하겠습니다.
글을 읽는 여러분이 고등학생이라면 그냥 가볍게 읽어보고 넘어가셔도 됩니다.
이 글이 필요한 학생은
1. 미분과 적분의 개념을 알고 있는 학생.
2. 구의 겉넓이를 구하는 과정을 알고 싶은 학생
3. 이중적분은 어떻게 사용되는 지 알고싶은 학생.
입니다.
제 글이 많은 학생들에게 도움이 됐으면 하는 바람입니다.
그럼 포스팅 시작합니다.
구의 겉넓이
구(sphere)란 공간좌표계의 한 정점으로부터 같은 거리에 있는 점들의 집합입니다.
(*평면좌표계의 한 정점으로부터 같은 거리에 있는 점들의 집합은 원(circle)입니다.)
구의 반지름을 R이라고 할 때, 겉넓이 S는 4πR² 으로 주어집니다.
공식 유도
구의 겉넓이를 구하기 위해서는 미분과 적분의 개념을 알고있어야 합니다.
미분은 어떤 요소를 한없이 작게 쪼개는 과정이고,
적분은 쪼개어진 요소 요소를 모으는 과정입니다.
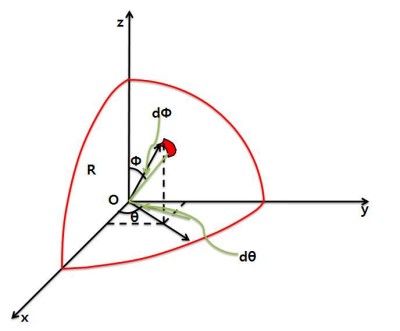
i) 구의 표면의 미소입자를 미소단위로 표현하기.
– 구형좌표계를 도입해서 미소입자를 나타내기
이제 우리는 구를 한없이 잘게 쪼개어 작은 입자들을 만들것입니다.(미분)
x, y, z축으로 이뤄진 공간좌표계(이를 데카르트 좌표계라 합니다.)에
중심이 원점, 반지름이 R인 구를 생각해봅시다.
편의상 그 구의 1/8과 구 위의 한 점을 그림으로 나타내면 아래와 같습니다.
좌표계에는 구형좌표계(spherical coordinate)라는 또다른 좌표계가 있습니다.
지금부터는 이를 도입하겠습니다.
위 그림에 나타난 구 위의 한 점에 대해서
점의 xy평면 위로의 정사영이 x축과 양의 방향으로 이루어 진 각의 크기를 θ,
화살표로 표현된 점의 위치벡터를 r축이라 하고,
z축으로부터 r축까지의 각도를 Φ(Phi)라고 해봅시다.
구형좌표계의 각 요소를 그림으로 표현하면 아래와 같이 됩니다.
구 위의 점에서 θ, Φ방향으로 매우 작은 각도만큼 선을 그어 보겠습니다.
그 각도를 dθ, dΦ 라 합시다.
(이처럼 수학에서 매우 작은 요소를 표현할때는 소문자 d를 이용합니다.
d는 differentiation(미분)의 d로, f'(x)를 dy/dx로 표현할 때 쓰는 그 d 입니다.)
이를 그림으로 표현하면 아래와 같습니다.
– 미소입자의 넓이 구하기
이제 구를 매우 잘게 쪼갰습니다. 위 그림에 나타난 붉은색 도형이 바로 구를 한없이 잘개 쪼갰을 때 생기는 미소입자입니다.
이 도형을 확대해보면 다음과 같습니다.
이제 이 도형의 각 변의 길이를 구해야하는데요.
부채꼴의 호의 길이를 구하는 공식으로 다음 공식이 있습니다.
이를 위 그림에 적용하면,
미소입자의 각 변의 길이는 각각 RdΦ, RsinΦdθ 로 구해집니다.
따라서 입자의 넓이를 dS라고 두면,
dS는 RdΦ와 RsinΦdθ의 곱입니다.
ii) 미소입자를 적분하기.
이제 위에서 구한 미소입자들을 한데 모아 더해봅시다.
각 위치별로 생기는 모든 입자들의 넓이의 합이 바로 구의 겉넓이가 될 것입니다.
앞에서 도입한 구형좌표계 그림을 가져와봅시다. 아래 그림은 전체 구의 1/8 부분만큼 해당하는 그림입니다. 그림에서 보이는 점이 미소입자를 구했던 위치입니다.
구 표면에 존재하는 모든 점들을 어떻게하면 표현할 수 있을까요?
구형좌표계의 θ와 Φ를 각각 0≤θ≤2π, 0≤Φ≤π 의 범위만큼 움직이하면 됩니다.
(이로써 구형좌표계를 도입한 이유를 설명할 수 있습니다. 데카르트 좌표계의 x, y, z로는 구 표면 위에 존재하는 모든 점을 x, y, z의 범위로 나타내기가 여간 까다로운 게 아닙니다.)
이제 모든 위치(0≤θ≤2π, 0≤Φ≤π )에서 생기는 모든 미소입자들의 합을 구해봅시다.
작은 요소 요소들을 더한다는 것은 적분의 개념입니다.
구 전체의 겉넓이를 S라 두면, 다음 수식을 세울 수 있습니다.
위에서 보이는 게 이중적분입니다.
이중적분은 별다른 게 아니라 차례차례 단일적분계산을 해주면 됩니다.
안쪽에 있는 적분을 먼저 해 줍시다.
이 결과를 이중적분속에 넣으면,
따라서 구의 겉넓이 S는 4πR² 임을 얻을 수 있습니다.
정리
이번 포스팅에서는
구의 겉넓이 공식 유도를 해보았습니다.
그 과정에서 미분과 적분의 개념을, 다소 직관적인 방법으로 설명했습니다.
이처럼 어떤 도형의 넓이를 구한다는 것은
i) 도형을 무수히 많은 미소입자로 잘게 쪼갠 뒤(미분)
ii) 그 미소입자의 넓이를 모두 합한다(적분)
는 뜻입니다.
구의 겉넓이를 구하는 과정은 고교 수학 범위를 넘어갑니다.
그러나 그 결과 (S=4πR² ) 만큼은 꼭 기억하고 있어야합니다.
728×90
구의 부피 / 겉넓이 공식 정리 (+예시 풀이)
반응형
안녕하세요. 훈릴스입니다.
오늘은 구의 부피와 겉넓이를 구하는 공식에 대해 알아보는 시간을 가져보고자 합니다. 공식이 어려운 것은 아닌데 자꾸 잊어버리는 분들이 많을 것으로 생각됩니다. 저와 오늘 같이 정리해보면서 확실하게 익혀봅시다! 레츠게릿!
구의 중심으로부터 구의 겉까지의 거리가 반지름입니다. 여기서는 반지름을 r이라고 표현을 했습니다. 위와 같이 구의 부피와 겉넓이의 공식은 다음과 같습니다. 많은 분들이 어떻게 저 공식이 나왔는지 궁금해하실 것으로 생각됩니다. 저 공식은 “적분”을 이용해서 구한 공식인데요. 아직까지 미분 / 적분을 이야기 하는 것은 너무 심오한 이야기가 되기에, 간단하게 구의 부피와 겉넓이는 저렇다라는 것만 인지하고 가시면 좋을 것 같습니다.
그렇다면 이번에는 반지름이 2인 구의 부피와 겉넓이는 어떻게 구할까요? 한 번 같이 문제를 풀어봅시다.
Q. 반지름이 2인 구가 있다. 이 구의 부피와 겉넓이는 어떻게 되는가?
우선 먼저 구의 부피를 구해봅시다. 앞서 알아본 바와 같이 구의 부피를 구하는 공식은 다음과 같습니다.
그렇기에 이러한 공식을 바로 적용해서 풀이를 하고자 합니다. 여기서 Pi는 계산하지 무한소수이기에 계산하지 않아도 좋습니다. 중학교 수준에서는 보통 3.14라고 생각하고 계산을 하는 경우가 많은데, 정확하게는 무한소수이기에 특정한 수로 표현하는 것은 틀렸습니다.
위의 그림과 같이 구의 부피를 구할 수 있습니다. 그렇다면 구의 겉넓이는 어떻게 구할까요? 바로 앞서 알아본 구의 겉넓이 공식을 사용하면 됩니다.
위의 공식을 사용할 때도, pi는 계산하지 않는 것이 옳습니다. 왜냐하면 3.14로 계산하는 것은 정확한 수치와는 상반되기 때문이죠. 하지만, 중학교 수준에서는 계산하라고 하는데 문제에서 pi=3.14라는 조건이 주어지면 계산하셔야해요! 이번 풀이에서는 계산하지 않고 pi로 그대로 나두겠습니다.
위의 그림과 같이 구의 겉넓이를 구할 수 있습니다. 사실 공식만 알면 곱하기만 해주면 되는 것이기 때문에 어려운 문제는 아닙니다. 하지만, 가끔식 마주하는 문제이기 때문에 공식을 잊어버리는 분들이 많을 것으로 생각돼요. 연습장에 10번씩 쓰면서 뇌 깊숙히 기억하도록 합시다!! 이상입니다.
반응형
구의 부피와 구의 겉넓이
이 글에서 공부할 내용은 구의 부피와 구의 겉넓이입니다.
구의 부피와 구의 겉넓이
구는 축구공, 배구공처럼 둥근 공 모양을 구하고 하지요? 구는 밑면, 옆면 구분이 없어요. 그래서 전개도로 펼쳐서 구하지 않아요.
구의 부피부터 구해보죠.
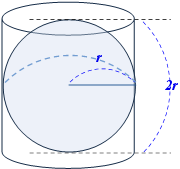
원뿔의 부피는 원기둥의 부피의 이었어요. 구는 원기둥 부피의 입니다.
원기둥의 부피의 인데, 이때의 원기둥의 높이는 얼마일까요? 구의 반지름이 r이라고 하면 원기둥의 높이는 2r, 즉 구의 지름의 길이와 같아요.
원기둥의 부피 공식에서 높이에는 2r을 넣어주고, 를 곱해주면 구의 부피를 구할 수 있어요.
πr2h → πr2 × 2r
= πr3
구의 겉넓이는 구의 부피와 각뿔의 부피를 이용해서 구하는데, 그 과정이 조금 어려워요. 공식 구하는 과정은 고등학교 올라가면 자연스럽게 알게 될 거니가 여기서는 그냥 결과만 얘기할게요.
구의 겉넓이는 4πr2입니다.
구의 반지름이 r일 때
구의 부피 = πr3
구의 겉넓이 = 4πr2
잘 보세요. 구의 부피는 마지막이 r의 세제곱이고, 구의 겉넓이는 r의 제곱이에요. 착각하지 마세요.
반지름이 6cm인 반구가 있다. 이 반구의 겉넓이와 부피를 구하여라.
반구는 구가 반으로 잘린 걸 말해요.
먼저 부피를 구해보죠. 반구는 원래 구의 반이니까 부피도 절반이겠죠?
반구의 부피 = 구의 부피 ÷ 2
= πr3 ÷ 2
= π63 ÷ 2
= 144π(cm3)
반구의 겉넓이는 구의 겉넓이의 절반이에요. 그런데 반구에서 잘린 면이 있지요? 이 면의 넓이를 더해줘야 해요. 이 잘린 면은 원이네요.
반구의 겉넓이는 = 구의 겉넓이 ÷ 2 + 잘린 면의 넓이
= 4πr2 ÷ 2 + πr2
= 4π62 ÷ 2 + π62
= 72π + 36π
= 108π(cm2)
함께 보면 좋은 글
원기둥의 부피와 겉넓이, 각기둥의 부피와 겉넓이
원뿔의 겉넓이와 부피, 각뿔의 겉넓이와 부피
원주율, 원의 둘레, 원의 넓이, 부채꼴 호의 길이, 부채꼴 넓이
정리해볼까요 구의 겉넓이와 부피 구의 반지름이 r일 때
구의 부피 = π r³
r³ 구의 겉넓이 = 4 π r2
그리드형(광고전용)
So you have finished reading the 구의 겉 넓이 적분 topic article, if you find this article useful, please share it. Thank you very much. See more: 구의 겉넓이 구분구적법, 구의 겉넓이 공식, 구의 표면적 공식, 구의 겉넓이 중학교, 구의 부피 공식 증명, 구의 넓이, 반구 겉넓이, 원기둥의 겉넓이 공식

